Empirical process
The study of empirical processes is a branch of mathematical statistics and a sub-area of probability theory. It is a generalization of the central limit theorem for empirical measures. Applications of the theory of empirical processes arise in non-parametric statistics.
Contents |
Definition
It is known that under certain conditions empirical measures 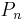 uniformly converge to the probability measure P (see Glivenko–Cantelli theorem). The theory of Empirical processes provides the rate of this convergence.
uniformly converge to the probability measure P (see Glivenko–Cantelli theorem). The theory of Empirical processes provides the rate of this convergence.
A centered and scaled version of the empirical measure is the signed measure
It induces a map on measurable functions f given by
By the central limit theorem, 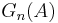 converges in distribution to a normal random variable N(0, P(A)(1 − P(A))) for fixed measurable set A. Similarly, for a fixed function f,
converges in distribution to a normal random variable N(0, P(A)(1 − P(A))) for fixed measurable set A. Similarly, for a fixed function f, 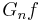 converges in distribution to a normal random variable
converges in distribution to a normal random variable 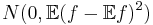 , provided that
, provided that 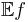 and
and 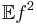 exist.
exist.
Definition
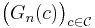 is called an empirical process indexed by
is called an empirical process indexed by 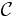 , a collection of measurable subsets of S.
, a collection of measurable subsets of S.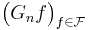 is called an empirical process indexed by
is called an empirical process indexed by 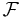 , a collection of measurable functions from S to
, a collection of measurable functions from S to  .
.
A significant result in the area of empirical processes is Donsker's theorem. It has led to a study of the Donsker classes such that empirical processes indexed by these classes converge weakly to a certain Gaussian process. It can be shown that the Donsker classes are Glivenko–Cantelli classes, the converse is not true in general.
Example
As an example, consider empirical distribution functions. For real-valued iid random variables 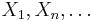 they are given by
they are given by
In this case, empirical processes are indexed by a class ![\mathcal{C}=\{(-\infty,x]:x\in\mathbb{R}\}.](/2012-wikipedia_en_all_nopic_01_2012/I/4fca1a7b215a1aa5cdbf96e6673cd628.png) It has been shown that
It has been shown that 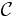 is a Donsker class, in particular,
is a Donsker class, in particular,
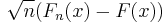 converges weakly in
converges weakly in 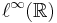 to a Brownian bridge B(F(x)) .
to a Brownian bridge B(F(x)) .
See also
References
- P. Billingsley, Probability and Measure, John Wiley and Sons, New York, third edition, 1995.
- M.D. Donsker, Justification and extension of Doob's heuristic approach to the Kolmogorov–Smirnov theorems, Annals of Mathematical Statistics, 23:277–281, 1952.
- R.M. Dudley, Central limit theorems for empirical measures, Annals of Probability, 6(6): 899–929, 1978.
- R.M. Dudley, Uniform Central Limit Theorems, Cambridge Studies in Advanced Mathematics, 63, Cambridge University Press, Cambridge, UK, 1999.
- M.R. Kosorok, Introduction to Empirical Processes and Semiparametric Inference, Springer, New York, 2008.
- Galen R. Shorack and Jon A. Wellner, Empirical Processes with Applications to Statistics, Wiley, New York, 1986. SIAM Classics edition (2009), Society for Industrial and Applied Mathematics. ISBN 978-0-898716-84-9
- Aad W. van der Vaart and Jon A. Wellner,Weak Convergence and Empirical Processes: With Applications to Statistics, 2nd ed., Springer, 2000. ISBN 978-0-387-94640-5
- J. Wolfowitz, Generalization of the theorem of Glivenko–Cantelli. Annals of Mathematical Statistics, 25, 131–138, 1954.
- K.O. Dzhaparidze and M.S. Nikulin, Probability distributions for the Kolmogorov and omega-square statistics for continuous distributions with scale and shift parameters, Journal of Soviet Mathematics, 20(3):2147-2163, 1982.
External links
- Empirical Processes: Theory and Applications, by David Pollard, a textbook available online.
- Introduction to Empirical Processes and Semiparametric Inference, by Michael Kosorok, another textbook available online.
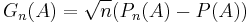
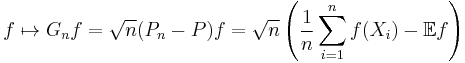
![F_n(x)=P_n((-\infty,x])=P_nI_{(-\infty,x]}.](/2012-wikipedia_en_all_nopic_01_2012/I/b46a6b6ef0d1c2b968194ccfba575624.png)